Volume and MEASUREMENT test
Friday the 5th grade is taking a test on their volume and measurement. This test will be given on Friday may 15th. This week the students will study for this test. Here are the standards for the test.
- Geometry 5.G.B.3 - 4
- I can understand how attributes of 2-dimensional shapes in a category also belong to all subcategories of those shapes.
- I can classify 2-dimensional shapes based on their properties.
- Measurement & Data 5.MD.A.1 (CONVERSIONS)
- I can convert different-sized measurements within the same measurement system.
- I can use measurement conversions to solve real-world problems.
- Measurement & Data 5.MD.C.3 - 5 (VOLUME)
- I can recognize volume as a characteristic of solid figures and understand how it can be measured.
- I can understand a "unit cube" as a cube with side lengths of 1 unit and can use it to measure volume.
- I can solve real-world problems involving volume by thinking about multiplication of addition.
- I can solve real-world and mathematical problems involving volume of an object using the formulas V = l x w x h and V = b x h
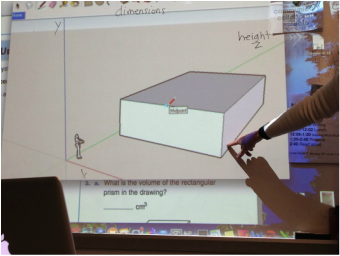
5 object volume project
The 5th grade this week is working on finding the volume of five objects. The students went around the classroom and picked out 5 different objects. They are finding the volume and making 3D drawings of the objects on isometric graph paper. They are putting the 3D drawings into a booklet.
area and volume
2 Dimensional and 3 Dimensional are very different dimensions. 2D shapes are flat and the formula is length times width. We use area to find the volume of 3D shapes. Volume is 3D, the formula for a box shape is length times width times height. The formula for a cylinder is π × r2 ( pi times radius squared) times height. To find the volume of a cylinder, you must use the formula stated above. Then you multiply the answer of the formula by the height of the cylinder. There is a fourth dimension, which is time and that makes the shape a hologram but we are not learning about the fourth dimension this year. We have been learning this all year and we are getting better and better at geometry.
FRACTIONS-DECIMALS-PERCENTS
Fractions, decimals and percents are all related. They help us understand the "in-between" numbers involved in math and statistics. They all can be determined by using each other. A fraction is simply a portion of a whole number. For instance, 3/4 is a fraction. If a whole were split into 4 equal parts and 3 of those parts were separated, that would be how 3/4 would be represented. Written in decimal form, 3/4 is equal to 0.75. That decimal can be found by dividing 3 by 4. When 3 is divided 4 equal times, each part is 0.75. To find the percent, we take the decimal and multiply by 100. In this case, 0.75x100 is 75%. So 3/4, 0.75, and 75% are all the same number represented in three different forms. The video below is an example of how we use Educreations in class to model our learning.
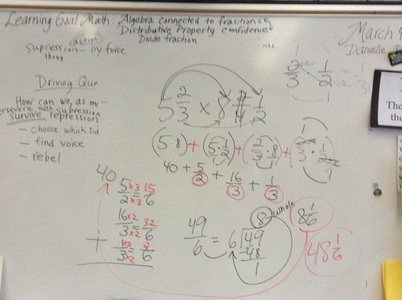
Dividing Fractions by whole numbers
"Multiply the Reciprocal"
The problem is 2 divided by 1/2. First you make the whole number a improper fraction. 2=4/2. Make sure you multiply by the reciprocal. You get 4/2x2/1. Multiply the problem. You get 8/2. Simplify and you get a whole number of 4. In the video below, the original problem should have been written: 2 divided by 1/2. Then 2 = 4/2 rather than 4 = 4/2. The rest is solved correctly.
The problem is 2 divided by 1/2. First you make the whole number a improper fraction. 2=4/2. Make sure you multiply by the reciprocal. You get 4/2x2/1. Multiply the problem. You get 8/2. Simplify and you get a whole number of 4. In the video below, the original problem should have been written: 2 divided by 1/2. Then 2 = 4/2 rather than 4 = 4/2. The rest is solved correctly.
Multiplying Fractions and Mixed Numbers
Lately the 5th grade has been working hard on learn how to multiplying fractions. One method is cross multiplying. Which is multiplying the numerator by the numerator and the denominator by the denominator. You can also multiply mixed numbers.
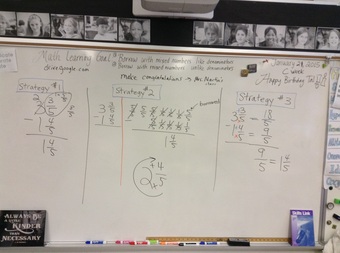
adding fractions
with un-like
denominators
Imagine that you have the fraction problem 7/8+2/7 written vertical. Since they have to different denominators. You have to times the denominator with the other. Example: 7/8 times both
the numerator and the denominator by 7. 2/7 times both the numerator and denominator. Then you get the fractions 49/56+14/56. The answer to the problem is 63/56. So 49/56+14/56=63/56.
the numerator and the denominator by 7. 2/7 times both the numerator and denominator. Then you get the fractions 49/56+14/56. The answer to the problem is 63/56. So 49/56+14/56=63/56.
Fractions
Multiply, Divide, Subtraction, and Addition. Everything about fractions is important. During the month of February we are learning two ways to multiply. The visual and multiply across. The visual (shown down below) is when we draw a square in our blue math notebook and divide the square in two how many parts have in the first denominator of the first fraction horizontally. THen we do the same for the second denominator vertically. We color in amount of the fraction we need both horizontally and vertically. We count how many smaller squares (that we just made) that are colored with both colors. THe multiplying across strategy is when you multiply the two denominators together and the two numerators together. We have to work on fractions because when we are out of school no one is going to help us when we are trying to multiply two ingredients for a recipe.
Algebra
In class we have been learning about algebra a problem we would try to solve would look like c*23=x and we would try to figure out what the missing number is.